A SEMI-ANALYTICAL MODEL FOR

PLANETARY RESONANCES

Planets around Single and Binary Stars
with arbitrary eccentricities and inclinations

Tabare Gallardo^1, Cristian Beauge^2, Cristian Giuppone^2
1: Departamento Astronomia, Facultad de Ciencias, Uruguay
2: Universidad Nacional de Cordoba, Observatorio Astronomico - IATE, Argentina
www.fisica.edu.uy/~gallardo/atlas/plares.html

Reference: Gallardo, Beauge and Giuppone, 2021, Astron. Astrophys. 646, A148, (ArXiv).


The present codes reproduce a model that describes the resonance strength, width, location and stability of fixed points (libration centers), as well as periods of small-amplitude librations. The model is valid to any two gravitationally interacting massive bodies orbiting another massive body, and thus applicable to planets in mutual resonance around single stars or planets in resonance with binary stars. It can be applied to satellites around planets only when planetary oblateness can be ignored. The fundamental assumption of the model is that the longitude of perihelia and nodes remain approximately fixed during a libration period.



plares.zip: compressed file with various versions of the code in fortran. Version 26/01/2022.
See updated version at the main MMRs site

Given a system of N gravitationally interacting bodies, the codes allow to determine the resonant structure in a region of the phase space obtained, for example, by varying the initial conditions of one of its members.


Talks about the model:


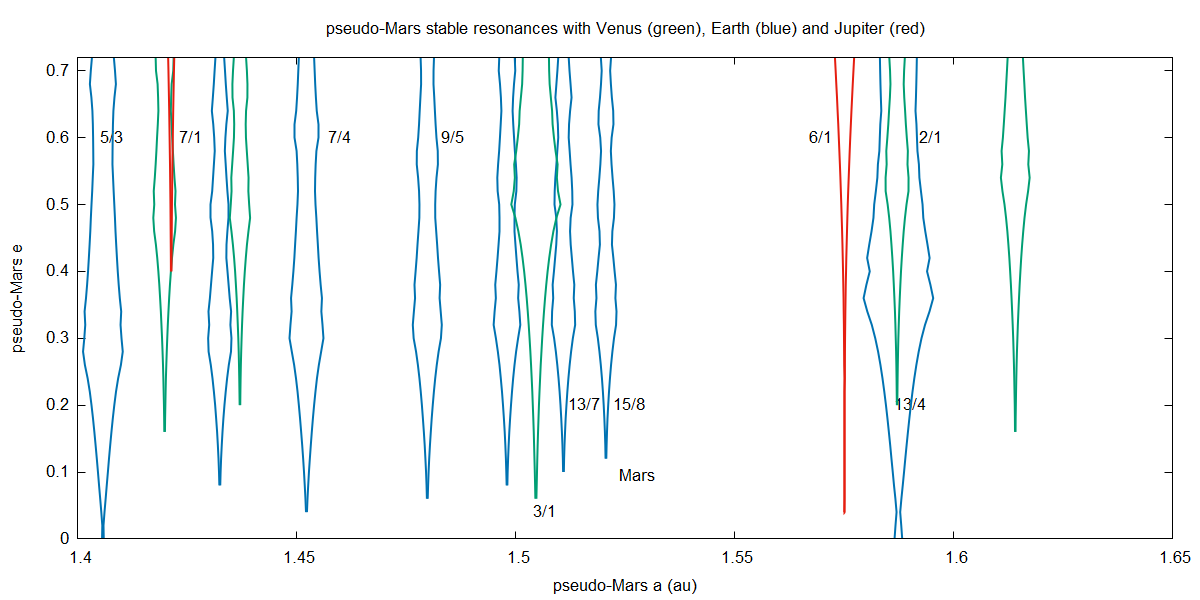
Example of what the program generates. Taking a "pseudo" planet Mars moving its position in semi-major axis and eccentricity, the code calculates the stable widths of the resonances with Venus (green), Earth (blue) and Jupiter (red). Two interesting things: a) the resonances with Venus and Earth are stronger, and b) note that Mars is located in a region relatively void of strong resonances (its actual position is indicated). Note: "stable width" means maximum resonance width avoiding close encounters to less than 3 mutual Hill sphere radius.
Input and output files for generating this plot here.


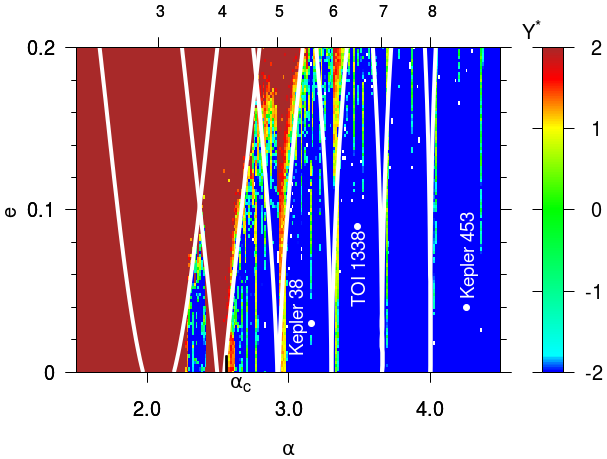
Another example. Megno map in the (a,e) plane for a planet in resonance with a binary star. Dark blue corresponds to more regular orbits, and lighter tones of green indicate increasingly chaotic motion. Brown corresponds to ejections. The libration widths of the most relevant MMRs determined with the model are plotted as white lines. The top scale indicates the positions of N/1 resonances with respect to the mean motion of the binary. Additionally, we plot the position of some similar circumbinary systems. Taken from Gallardo, Beauge and Giuppone (2021).


Back to the web atlas of resonances