COLISIONLAB

LABORATORIO VIRTUAL DE COLISIONES

de cuerpos menores con planetas

Tabaré Gallardo - Departamento de Astronomía - Instituto de Física - Facultad de Ciencias - Uruguay

version febrero de 2018
DESCRIPCION

Este programa (colisionlab.exe) nos brinda la información necesaria para calcular la probabilidad de que un asteroide o cometa (o un auto!) colisione con un planeta (desde Mercurio a Neptuno). Esta probabilidad la podremos calcular en base a la lista de encuentros asteroide-planeta que registrará el programa. Utilizando el programa auxiliar grafica.exe podemos visualizar la distribución espacial de los encuentros respecto al planeta y utilizando evolucion.exe podemos visualizar la evolución de la órbita del asteroide debido a las perturbaciones generadas por el planeta. El programa calcula numericamente la evolucion orbital heliocentrica del asteroide perturbado por el planeta considerado. Solo se considera un unico planeta en el sistema.
Este programa fue concebido como un laboratorio virtual para estudiantes de enseñanza media y universitarios.

Descargar COLISIONLAB.ZIP


PRIMER PASO: ejecución del programa colisionlab.exe

Hacemos doble clic en colisionlab.exe y elegimos el planeta (con un número del 1 al 8) con quien simularemos los encuentros. Luego el programa solicita los elementos orbitales del asteroide:

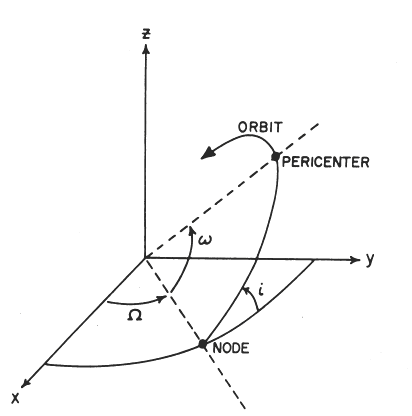
Inclinación (i), longitud del nodo (Omega) y argumento del perihelio (w). El plano XY es el plano de la eclíptica. Figura tomada de Greenberg 1982, Astron.J. 87, 184.


Todos estos elementos pueden encontrarse en catálogos o en internet (http://ssd.jpl.nasa.gov/sbdb.cgi), o también pueden utilizarse datos ficticios de forma de explorar con diferentes tipos de órbitas. Para que exista aproximación entre el asteroide y el planeta la órbita del asteroide no puede ser arbitraria. Se necesita que ambas órbitas se aproximen en algún punto del espacio. La proximidad de las órbitas esta dada por el MOID (Minimum Orbit Intersection Distance) que este programa calculará en Unidades Astronómicas y en radios planetarios. Si el MOID resulta muy grande probablemente no habrá encuentros por lo que el programa nos preguntará si no deseamos intentar con otro asteroide, debemos contestar S o N. Si decidimos seguir adelante con los cálculos el programa solicitará la posición inicial del asteroide dentro de su órbita (la anomalía media). Este valor lo podemos tomar aleatoriamente entre 0 y 360, o podemos utilizar el valor correspondiente. El programa comenzará a calcular la evolución orbital del asteroide debido a las perturbaciones del planeta y los detalles de la geometría de los encuentros con el planeta. Cada vez que el programa detecta un encuentro calcula y muestra en pantalla: Todos estos datos se almacenan también en el archivo encuentros.txt que puede abrirse con cualquier editor de texto elemental (preferentemente Textpad o Bloc de Notas). Si no se producen encuentros el programa mostrará simplemente el tiempo transcurrido en años y el MOID en UAs. Este variará debido a las perturbaciones que el planeta ejerce sobre la órbita del asteroide. Si crece llegará un momento en que los encuentros cesan hasta que vuelva a disminuir. Se puede esperar a que el programa realice toda la integración numérica predeterminada o puede interrumpirse en cualquier momento mediante CTRL-C. Si el asteroide colisiona con el planeta, con el Sol o es eyectado del sistema el programa se detiene.


SEGUNDO PASO: análisis de los resultados (grafica.exe y encuentros.txt)

Si queremos visualizar la distribución espacial de los encuentros hacemos doble clic en grafica.exe que nos muestra cómo el asteroide se presenta frente al planeta (ubicado en el origen) en el momento de la mínima distancia. El eje horizontal pertenece al plano de la eclíptica y la velocidad del asteroide es perpendicular a la pantalla en sentido entrante.

Como puede visualizarse en el ejemplo de la figura luego de muchos encuentros la distribución es aproximadamente homogénea, como si fuera producida por un tiro al blanco sin punteria aunque si los encuentros son escasos se puede distinguir alguna región más densa.


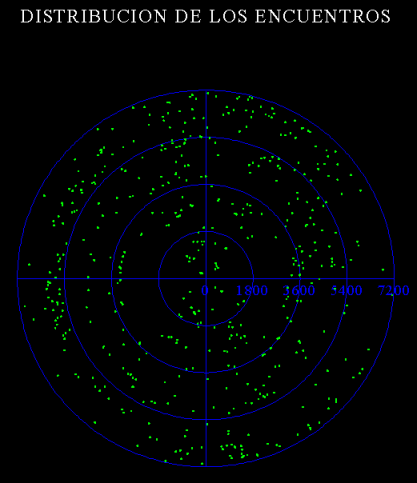
Ejemplo: distribución de encuentros de un transneptuniano con Neptuno. Distancia al centro del planeta en radios planetarios desde 0 a 7200.


Aún si la distribución no es uniforme se puede demostrar (Teoria de Opik) que el número de encuentros es aproximadamente proporcional al área considerada (o sea, a la distancia al cuadrado) lo cual es equivalente a suponer una distribución uniforma de puntos de encuentro en el plano de la figura. A partir de la hipótesis de distribución uniforme (igual numero de puntos por unidad de area) podemos estimar la probabilidad de colisión en el lapso T en que se realizó la simulación. Para esto, analizando el archivo encuentros.txt:
  1. Elegimos una distancia límite Dlim (está expresada en radios planetarios)

  2. Contamos todos los encuentros a menos de esa distancia límite N(D < Dlim)

  3. Calculamos la probabilidad de colisión Pcol, para eso realizamos la siguiente regla de tres: 
    
area circulo radio Dlim -------> N encuentros

area circulo radio sigma ---------> X encuentros

               sigma^2
de donde: X =  ------- N
               Dlim^2
    Sigma es el "parametro de impacto" correspondiente a la colision que es la distancia al planeta a partir de la cual el impacto sera inevitable debido al enfoque gravitatorio del planeta. X será el número de encuentros a menos de una distancia igual al parametro de impacto, es decir, X es el número de colisiones esperadas en el lapso T. O sea que X es Pcol. El sigma de colision esta estimado en la ultima columna del archivo encuentros.txt.

  4. Generalmente Pcol es un numero menor que 1 así que deberíamos calcular el tiempo necesario para que Pcol=1 (probabilidad = 1 significa certeza de colisión). A este tiempo se le llama Vida Media Colisional del asteroide y también lo calculamos por una regla de tres: 
    
lapso T ---------> Pcol

lapso VMC -------->  1

                                         T
de donde simplemente:    VidaMediaCol = ----
                                        Pcol
    Esta vida media así calculada estará en años y es el tiempo medio esperado para que el asteroide colisione con el planeta.

AFINANDO EL CALCULO DE LA VIDA MEDIA
La evolución orbital por encuentros es sumamente caótica por lo que para tener una idea más precisa de la Vida Media del asteroide y de la Probabilidad de Colisión con el planeta es aconsejable repetir el experimento con posiciones iniciales diferentes del asteroide en su órbita (diferente anomalía media inicial). De esta forma se obtendrá una nueva vida media, y repitiendo varias veces el procedimiento tendremos una idea más realista de la Vida Media y de los márgenes entre los que puede encontrarse.

RADIANTE Y PROBABILIDAD DE EYECCION
Si la velocidad de encuentro asteroide-planeta es alta la orbita se va modificando muy lentamente por lo que las circunstancias de los encuentros como la dirección de donde se vería surgir el asteroide (radiante) se mantienen con leves variaciones.
Los planetas de masa grande como Júpiter en cambio producen grandes variaciones orbitales y en particular la probabilidad de eyección del Sistema Solar no es despreciable y puede llegar a ser mucho mayor que Pcol. Repitiendo varias veces el experimento con un asteroide (o cometa) podemos evaluar ambas probabilidades (colisión y eyección) y conocer en definitiva cuál será el final más probable para el objeto. La probabilidad de eyección depende de los parametros orbitales (a,e,i) del asteroide y en algunos casos la eyección es imposible.

CAPTURA
Con planetas gigantes como Júpiter puede ocurrir ocasionalmente que se obtienen muchos encuentros a pequeñas distancias del planeta y separados por muy poco tiempo (uno o dos años tal vez). Esto es debido a un interesante y raro fenomeno: el planeta ha capturado temporariamente al asteroide o cometa como si fuera un satélite y lo que el programa registra son los sucesivos pasajes por el periastro planetocéntrico.

TERCER PASO: evolución orbital con evolorb.txt y evolucion.exe

El programa también genera el archivo evolorb.txt que puede abrirse con cualquier editor conteniendo la evolución en el tiempo de los elementos orbitales a, e, i, longitud del nodo, argumento del perihelio y tambien el MOID. Estos elementos varían debido a las perturbaciones gravitacionales del planeta.
La evolución en el tiempo de la órbita puede visualizarse ejecutando evolucion.exe que abre una ventana con los siguientes elementos: El programa mostrará la animación correspondiente al período de tiempo calculado.


EJEMPLO: encuentros del auto Tesla Roadster con la Tierra

Si ejecutamos el programa e introducimos los datos orbitales de este auto (!): 
 a (ua)     :  1.331
 e          :  0.26
 i          :  1.09
 long. nodo :  317
 arg. peri. :  177
el programa nos dirá que el MOID es 0.000797 ua lo cual es una distancia muy pequeña que garantiza que existiran encuentros con la Tierra. Para la posición inicial lo pondremos en anomalía media = 6.33 y el programa comenzará a calcular los encuentros. Al llegar a los 100.000 años aproximadamente cortamos el programa con CTRL C. Si vamos al archivo encuentros.txt veremos lo siguiente: 
 -----------------------------------------------------
 DATOS DEL ASTEROIDE:
 a (ua)     :  1.331
 e          :  0.26
 i          :  1.09
 long. nodo :  317.
 arg. peri. :  177.
 MOID (ua)  :  0.000797153573
 pos. inic. :  6.33
 REGISTRO DE ENCUENTROS CON EL PLANETA Tierra
                                          radiante
  t(a¤os)    Dist/R  ang   V(Km/s)  Pla  lon.  lat.    sigma/R
       58.48    35.2  261.7   4.03    3   52.0   17.4      2.97
      406.47    46.1  219.7   3.95    3   63.0   28.2      3.02
      460.48   143.1   57.2   3.58    3   60.5   31.6      3.30
      761.46   160.1  155.4   3.84    3   71.5   23.7      3.10
     3312.60   216.7  175.0   3.88    3   42.2  -27.1      3.07
Si ejecutamos grafica.exe haciendo doble clic se genera la siguiente grafica mostrando la distribucion espacial de los encuentros con la Tierra.


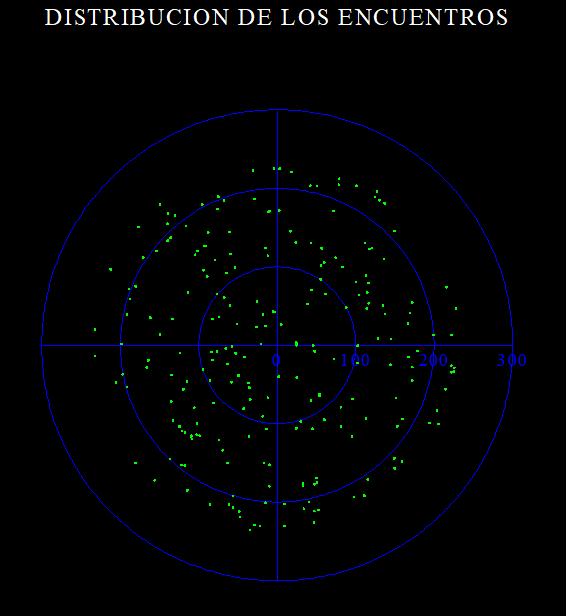
Distribución de encuentros del Tesla Roadster con la Tierra. Distancia al centro del planeta en radios planetarios.


En 100.000 años se detectaron 224 encuentros a menos de 236 radios terrestres, entonces: 

Dlim = 236 radios terrestres
sigma = 3.1 radios terrestres aprox

area circulo radio 236 -------> 224 encuentros

area circulo radio 3.2 ---------> X

               3.2^2
de donde: X =  ------- 224 = 0.041 encuentros en 100.000 años.
               236^2

                                        100.000
                        VidaMediaCol = -------- = 2.44 Millones de años
                                        0.041
De acuerdo a esta simulacion, ese seria el tiempo esperado hasta la colision con la Tierra. El experimento deberia repetirse con otros valores iniciales para la anomalia media.

EJEMPLO: encuentros del asteroide 3200 PHAETHON con la Tierra

Si ejecutamos el programa e introducimos los datos orbitales de este asteroide: 
 a (ua)     :  1.27
 e          :  0.89
 i          :  22.2
 long. nodo :  265.4
 arg. peri. :  322.
el programa nos dirá que el MOID es 0.02110 ua lo cual es una distancia razonable para que existan encuentros con la Tierra. Para la posición inicial lo pondremos en anomalía media = 0 (en perihelio) y el programa comenzará a calcular los encuentros. Si vamos al archivo encuentros.txt veremos lo siguiente: 
 -----------------------------------------------------
 DATOS DEL ASTEROIDE:
 a (ua)     :  1.27
 e          :  0.89
 i          :  22.2
 long. nodo :  265.4
 arg. peri. :  322.
 MOID (ua)  :  0.0211022164
 pos. inic. :  0.
 REGISTRO DE ENCUENTROS CON EL PLANETA Tierra
                                          radiante
  t(años)    Dist/R  ang   V(Km/s)  Pla  lon.  lat.    sigma/R
     7630.34   222.3    6.9  33.63    3  109.5   11.9      1.05
     7718.34   205.8   14.7  33.66    3  109.4   11.9      1.05
     7731.34   215.4   21.8  33.93    3  109.2   11.8      1.05
     8188.34   221.5   30.3  33.97    3  109.1   11.8      1.05
     8247.34   179.0   11.4  33.69    3  109.4   12.0      1.05
     8872.34   139.9   94.9  33.77    3  109.2   12.0      1.05
Puede verse que el radiante estaría en longitud eclíptica 109 grados y latitud eclíptica 12 grados que es un punto muy próximo a la estrella Castor de la constelación de Geminis. Ese es exactamente el radiante de las Gemínidas, una lluvia de meteoros generada por pequeños fragmentos eyectados de Phaethon. Se piensa que en realidad Phaethon es un cometa extinto. Con el transcurso del tiempo el radiante se irá desplazando lentamente en la esfera celeste.



OTRAS POSIBLES ACTIVIDADES a realizar con COLISIONLAB

GLOSARIO

MOID: Minimum Orbit Intersection Distance. Mínima distancia entre la elipse del asteroide y la del planeta. Varía en la medida de que la órbita del asteroide va evolucionando.

NEO: Near Earth Objects u "objetos cercanos a la Tierra" son asteroides o cometas con perihelio interior o próximo a la órbita terrestre

PHA: Potentially Hazardous Asteroids o "asteroides potencialmente peligrosos" (para la Tierra). Son asteroides de diámetro mayor que 150 metros (magnitud absoluta H < 22) cuyas órbitas pasan muy próximo de la órbita terrestre, o sea, tienen MOID pequeño (menor a 0.05 UAs). Ver pagina del JPL.

Probabilidad de Colisión y Vida Media: Con el transcurso de los años el asteroide se encontrará con el planeta a diferentes distancias. En cada pasaje su órbita será alterada por el planeta. La evolución orbital es tan caótica que es imposible predecir exactamente cuando ocurrirá una colisión. Pero podemos tener una idea estadística del evento de colisión. Podemos evaluar la probabilidad de que ocurra una colisión (Pcol) en un cierto lapso o podemos estimar el tiempo medio necesario que debe transcurrir para que ocurra una colisión del asteroide con el planeta (vida media del asteroide).

Radiante: Es la dirección espacial desde donde se vería aproximarse al asteroide. Si la órbita del asteroide no cambia demasiado el radiante se mantendrá aproximadamente constante. Pero debido a la evolución orbital del asteroide (o corriente meteórica) el radiante mostrará cierta variación en el transcurso de miles de años. Ver Corrientes meteoricas (del JPL) y el sitio de la International Meteor Organization.

Radio de Hill: región del espacio en donde la atracción gravitacional planetaria es suficientemente grande como para que el movimiento del asteroide pueda ser considerado planetocéntrico.

Teoría de Opik: antes de la época de las computadoras Opik desarrolló una teoría analítica sobre encuentros en donde, en pocas palabras, se demuestra que el número de encuentros a menos de una cierta distancia es aproximadamente proporcional al cuadrado de la distancia.

ALGUNOS VINCULOS

How to deal with impacting bodies , actividad en java de Joachim Köppen Kiel
NEOs, del JPL.
MOIDs calculados para diversos planetas (Lowell Obs)
NeoDys
Planetary Data System Small Bodies Node (University Of Maryland)
IAU Minor Planet Center (Smithsonian Astrophyical Observatory)
European Asteroid Reseach Node
The Near-Earth Objects Page (The Planetary Society)
Earth Impact Effects, programa que calcula los efectos de un impacto.
LOS ASTEROIDES URUGUAYOS


COMENTARIOS FINALES

Los programas auxiliares sólo funcionan si se encuentran disponibles los archivos "grafica.in" y "evolorb.txt". Como se trata de un cálculo probabilístico con fines educativos la integración numérica de las órbitas se hace sobre un modelo gravitacional compuesto por el Sol, el planeta y el asteroide, es decir se desprecian los efectos gravitacionales de los demás planetas. El modelo se integra con una adaptación del integrador EVORB de A. Brunini y T. Gallardo. Los programas fueron escritos en fortran y compilados con g77 para sistema operativo Windows. Para los programas auxiliares se utilizaron las librerias gráficas disponibles DISLIN de Helmut Michels. Recuerde que éste es básicamente un programa simulador para trabajar en enseñanza. Si Ud desea calcular en forma precisa la evolución de un determinado objeto deberá usar otros programas como EVORB o Mercury por ejemplo.


Lista de algunos asteroides que se encuentran con los planetas 

Desig      a           e           i       lon nod   arg per     H    MOID(UA) Pla

K04X60Y   0.6402479   0.7967956  23.74483 122.70422 130.76487  18.90    0.0009 1
K04E09V   1.4708753   0.7802795  40.91506 172.58851 226.57724  17.80    0.0010 1
J91V00E   0.8908850   0.6645483   7.22057  62.05995 193.46095  18.10    0.0015 1
J99Y05K   0.8294123   0.5583010  16.74132 349.66470 292.73547  16.80    0.0015 1
K04H00C   0.7891697   0.5988647  28.98110 203.02820 159.32783  20.00    0.0016 1
K04R10U   0.9040085   0.6568443  15.91507 119.11899  65.14954  18.20    0.0017 1
K04Q02X   1.2862892   0.9026720  19.06495 320.34802 218.64235  21.70    0.0019 1
K00D01O   1.4269322   0.6806036   3.44470 336.07786 302.46871  20.40    0.0020 1
K01W15N   2.2741937   0.8332083  57.06638 244.41893  51.38218  19.40    0.0022 1
K01T44X   0.8747773   0.5460239  15.20329  57.85776 135.96193  19.10    0.0025 1
K01C36P   0.7144851   0.4073062  10.55144 331.00623 353.49931  23.70    0.0025 1
K04T10D   0.7511065   0.4425780   2.61971  48.49406 136.66407  22.10    0.0029 1
K02F03B   0.7614800   0.6018541  20.27029 203.66223 148.24433  16.40    0.0032 1

Desig      a           e           i       lon nod   arg per     H    MOID(UA) Pla
01862     1.4707022   0.5598273   6.35510  35.77328 285.78177  16.25    0.0020 2
02201     2.1714528   0.7132048   2.51696  76.61394  96.24459  15.25    0.0065 2
04581     1.0219907   0.3568877   4.90995 180.45015 255.11122  20.40    0.0060 2
05131     1.4860918   0.5695851  36.40178 110.45604 135.74886  14.10    0.0022 2
05590     0.9856593   0.2795788  14.18615 216.34488  34.40942  19.70    0.0035 2
05604     0.9272533   0.4053818   4.79698 312.00859  82.41635  16.40    0.0058 2
08035     1.3418680   0.4623658  28.30850 185.68640   5.98712  17.30    0.0008 2
08176     1.5751881   0.6427368  39.62769  66.65488 241.80426  17.10    0.0087 2
65679     0.9148016   0.2646399   1.29135 178.35966  14.92238  19.40    0.0038 2
69230     1.6554162   0.6239970   6.06800  34.50962  92.39994  17.50    0.0048 2
85182     2.2140694   0.7804467   3.19074 341.47041 241.04664  17.10    0.0017 2
A1869     1.6235914   0.6111113   4.76438 111.16198 268.52932  19.30    0.0032 2

Desig      a           e           i       lon nod   arg per     H    MOID(UA) Pla
01981     1.7761202   0.6501591  39.83793 357.03664 267.73758  15.50    0.0040 3
02201     2.1714528   0.7132048   2.51696  76.61394  96.24459  15.25    0.0017 3
02340     0.8438658   0.4499335   5.85406 211.52604  39.93036  19.20    0.0070 3
04179     2.5252790   0.6342869   0.44680 123.19496 279.77015  15.30    0.0057 3
04581     1.0219907   0.3568877   4.90995 180.45015 255.11122  20.40    0.0033 3
04660     1.4887330   0.3599680   1.43211 314.53274 157.90472  18.20    0.0031 3
05693     1.2714445   0.5852633   5.05507  97.14311 258.77174  17.00    0.0054 3
07482     1.3462902   0.3281797  33.49011 117.93740  47.57721  16.80    0.0002 3
07753     1.4673394   0.4815481   3.12449  73.51168 279.97822  18.60    0.0067 3
20425     1.5647769   0.4763857   6.97766 227.52827 295.96169  20.40    0.0030 3
27002     1.7437385   0.4332551   8.69390 130.44781   0.65905  18.20    0.0032 3

Desig      a           e           i       lon nod   arg per     H    MOID(UA) Pla
01863     2.2592925   0.6067881  18.40100 346.60349 267.97081  15.54    0.0021 4
02101     1.8746514   0.7646234   1.34407 350.49007  42.56764  18.70    0.0071 4
02135     1.5995758   0.5030624  23.04966 191.33124 290.75717  17.94    0.0046 4
02201     2.1714528   0.7132048   2.51696  76.61394  96.24459  15.25    0.0090 4
03040     1.8407353   0.2005400  46.63822 143.56035 290.19949  14.50    0.0025 4
04503     2.6976409   0.5271099   2.51891  46.18894  76.23213  15.60    0.0085 4
05261     1.5235604   0.0647995  20.28186 245.09755  95.48672  16.10    0.0008 4
05641     1.8194695   0.1263187  22.20307 151.38438  56.89272  12.70    0.0040 4
05645     1.3549387   0.3873920  13.51198  45.84314  48.06366  17.00    0.0057 4
05863     2.2207005   0.5074664  19.47152 169.06907 115.33377  15.50    0.0074 4
06178     2.8088598   0.5865165   4.30971  64.79002 127.17976  15.10    0.0022 4
08013     2.2002795   0.4309209   7.56545 105.68825 146.71165  16.60    0.0088 4

Desig      a           e           i       lon nod   arg per     H    MOID(UA) Pla
00617     5.2273121   0.1380641  22.03481  44.36237 307.69837   8.19    0.1984 5
00911     5.2529895   0.0658171  21.78987 338.01637  80.58785   7.89    0.1220 5
01143     5.2581366   0.0902497   3.13477 221.31452 235.62954   7.93    0.0844 5
01208     5.2365533   0.0910185  33.56507  48.55494 295.93099   8.99    0.0051 5
01404     5.3026064   0.1132516  18.00645 332.97512  59.36321   9.00    0.0448 5
01437     5.1584533   0.0434731  20.52545 315.83805 130.15050   8.30    0.2292 5
01583     5.1064707   0.0520719  28.55196 221.36877 186.55181   8.60    0.0538 5
01647     5.2322550   0.0225539   5.64406 240.37248 294.70181  10.30    0.1388 5
03688     3.2223052   0.4784058   2.55943  19.98837 138.07751  14.90    0.2364 5
02483     3.9668522   0.2759915   4.49807 252.15867 182.89655  10.80    0.2487 5
06144     4.7741391   0.3605741   5.86383 117.26620  95.02865  11.50    0.1926 5
13230     5.0559803   0.0608788   4.32975  53.81968  37.16913  11.30    0.0773 5
15539     5.3601000   0.0426226  27.83134 108.94741 330.43608   9.90    0.0483 5
22049     5.3628353   0.0586310   2.54320 203.37090 249.80584  11.90    0.0949 5
20461    23.8654503   0.8996058 160.41735 297.47421 102.82860  13.80    0.1771 5

Desig      a           e           i       lon nod   arg per     H    MOID(UA) Pla
31824    11.7819128   0.3833143   5.25492  87.21015 281.64522  10.10    0.1305 6
32532    10.6155518   0.1982702  20.38328 205.26238  86.22902   9.00    0.0134 6
60558    10.7699059   0.4555755   4.33367 173.31056 162.39349   9.50    0.2129 6
J99XE3X  17.9539246   0.4619002   6.77736 103.81964 215.73331   8.60    0.1410 6
K00D08G  10.7903306   0.7938960 129.31494 279.12328 222.22099  13.10    0.1200 6
K03C22C   7.3468941   0.4286793   6.40215 123.84489  38.04156  14.30    0.1021 6
K04P44A  14.1961063   0.7583652   3.28432 212.56568  72.77890  13.60    0.2879 6
K04RE1W   6.9201226   0.4926828   7.66852 164.36870 156.93361  14.40    0.2665 6
K05O00E  63.8788206   0.9522455  67.55610 153.23337 116.02845  13.70    0.2419 6

Desig      a           e           i       lon nod   arg per     H    MOID(UA) Pla
44594    32.1361287   0.4522853   2.62229 259.19727 144.44224   6.80    0.1505 7
87555    34.9386683   0.5643024   6.79157 330.14384 284.31000   8.20    0.0277 7
B9315    17.4047635   0.1751098  17.45810  16.28015 303.26022   9.60    0.2690 7

Desig      a           e           i       lon nod   arg per     H    MOID(UA) Pla
10370    25.2003180   0.2504449   4.14114 178.12634   6.83451   8.00    0.4698 8
32929    39.4919166   0.2604423   4.84209 342.09102  24.95765   7.50    0.1872 8
33128    33.3537848   0.3824640  14.24255 132.76587 282.86280   7.20    0.4862 8
33340    39.1478123   0.2503720   3.03694 127.97875 324.71095   6.50    0.0033 8
44594    32.1361287   0.4522853   2.62229 259.19727 144.44224   6.80    0.4945 8
87555    34.9386683   0.5643024   6.79157 330.14384 284.31000   8.20    0.3120 8
91133    39.6524045   0.2339297   5.93209  50.20834 180.90533   7.60    0.1627 8
C0181    32.2185128   0.1693693   2.72072 146.50174 248.41574   7.00    0.2979 8
J95H05M  39.8688985   0.2576242   4.80715 186.62388  59.42255   8.30    0.2463 8


H: magnitud absoluta